6. การวิเคราะห์ความสัมพันธ์เชิงฟังก์ชันระหว่างข้อมูล
6.1 ประโยชน์และการเขียนความสัมพันธ์เชิงฟังก์ชันระหว่างข้อมูล
การวิเคราะห์ความสัมพันธ์เชิงฟังก์ชันระหว่างข้อมูล
โดยปกติเราจะพบความสัมพันธ์ในรูปแบบ
ต่างๆเมื่อกำหนดสมการมาให้โดยมีค่า x และ y ซึ่ง x เป็นตัวแปรอิสระ
และ y เป็นตัวแปรตาม
เช่น กำหนดสมการที่มีความสัมพันธ์เป็นเส้นตรง y
= 2x+5 จงหาค่าของ y
เมื่อ x = 10 เป็นต้น
หรืออาจจะเป็นสมการพาราโบลา สมการเอกซ์โพเนนเชียลฯลฯ
แต่ในบทนี้โจทย์กำหนดความสัมพันธ์ระหว่าง x และ y
ให้ แล้วเราต้องสร้างสมการขึ้น
มาเอง เช่นกำหนดความสัมพันธ์ของ x และ y ดังนี้
x
|
0
|
1
|
2
|
3
|
4
|
y
|
2
|
5
|
7
|
10
|
11
|
ถ้า x เท่ากับ 8 แล้ว y มีค่าเท่ากับเท่าใด. ถ้าเราดูเฉพาะความสัมพันธ์ระหว่าง
x กับ y เราไม่สามารถหาค่า y ได้เมื่อ x = 8 เพราะฉะนั้นเราต้องสร้างสมการขึ้นมาก่อน การที่โจทย์กำหนด
ความสัมพันธ์ของ x และ y
มาให้เราจะต้องเขียนแผนภาพการกระจายดูก่อนว่ามีความสัมพันธ์
ลักษณะใด (ถ้าโจทย์บอกมาว่าเป็นความสัมพันธ์ลักษณะใดเราไม่ต้องเขียนแผนภาพการกระจาย)
ในการเขียนแผนภาพการกระจายเราเขียนคร่าวๆเพื่อดูแนวโน้มว่ามีความสัมพันธ์ลักษณะใด
เนื้อหาในบทนี้เราจะศึกษาเฉพาะความสัมพันธ์ที่มีลักษณะ
เส้นตรง พาราโบลา เอกซ็โพเนนเชียล
ตัวอย่างที่ 1 จากความสัมพันธ์ต่อไปนี้
จงเขียนแผนภาพการกระจายของความสัมพันธ์
x
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
y
|
2
|
3
|
3
|
4
|
5
|
7
|
8
|
วิธีทำ
ตัวอย่างที่ 2 ให้นักเรียนเขียนแผนภาพการกระจายของความสัมพันธ์ต่อไปนี้
x
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
y
|
14
|
10
|
6
|
4
|
3
|
4
|
5
|
6
|
10
|
 |
ตัวอย่างที่ 3 ให้นักเรียนเขียนแผนภาพการกระจายของความสัมพันธ์ต่อไปนี้
x
|
1
|
1.5
|
2
|
2.5
|
3
|
3.5
|
4
|
4.5
|
5
|
y
|
2
|
3
|
4
|
6
|
8
|
12
|
16
|
22
|
30
|
6.2 สมการความสัมพันธ์เชิงฟังก์ชันและการหาค่าคงตัวโดยใช้สมการปกติ ที่อยู่ในรูป
เส้นตรง พาราโบลาและเอกซ์โพเนนเชียล
พร้อมทั้งทำนายค่าตัวแปรตามเมื่อกำหนดตัวแปรอิสระ
6.2.1
สมการความสัมพันธ์เชิงฟังก์ชันที่อยู่ในรูปเส้นตรง
y = mx + cมีสมการเป็น
เมื่อ y คือตัวแปรตาม และ x คือตัวแปรอิสระ
เมื่อ y คือตัวแปรตาม และ x คือตัวแปรอิสระ
ตัดแกน Y เช่น y = 5x + 3 , m = 5
, c = 3
การที่เราจะสร้างสมการ y = mx + c ,มีตัวไม่ทราบค่า 2 ตัวคือ m กับ
c จึงจะต้องหาสมการปกติ
ของเส้นตรงคือ
ตัวอย่างที่ 1 จากความสัมพันธ์ของข้อมูลต่อไปนี้
ปริมาณปุ๋ย(กก./ไร่) ผลผลิต(กก./ไร่)
1
8
2
9
3
10
4
12
5
15
ก.
จงเขียนแผนภาพการกระจาย
ข.
ถ้าใส่ปุ๋ย 3.5 กก./ไร่ จะให้ผลผลิตเท่าใด.
วิธีทำ จากสมการเส้นตรง y
= mx + c หา m , c
จากสมการปกติ
สร้างตารางเพื่อแทนค่าในสมการปกติ
แทนค่าในสมการปกติจะได้ ……. =……. m
+…………c………………..(1)
…….
= ……m + …………c………………(2)
3(1), 162 =
45m + 15c………………(3)
(2) – (3), 17 = 10 m จะได้ m = 1.7
แทนค่า m
= 1.7 ใน (1) , จะได้ c = 5.7
แทนค่า m
= 1.7 และ c = 5.7 ลงในสมการรูปทั่วไป y = mx + c
จะได้สมการของความสัมพันธ์คือ y = ………x + …………
ถ้า x
= ………จะได้ y
= ……. (…….) + ……… = …………
แสดงว่าใส่ปุ๋ย ……… กก./ไร่ จะให้ผลผลิต ………. ….. กก./ไร่
ตัวอย่างที่ 2 จากการสอบถามถึงรายจ่ายของครอบครัว 8 ครอบครัวในท้องที่แห่งหนึ่งที่มีรายได้
ต่อเดือนตั้งแต่ครอบครัวละ 1,000 บาท ถึง 14,000 บาท ปรากฏผลดังตารางต่อไปนี้
ก. จงเขียนแผนภาพการกระจายของข้อมูล
ข. ถ้าครอบครัวในท้องที่นั้นมีรายได้
เดือนละ 5,000 บาท ให้ทำนายรายจ่ายของครอบครัวนั้น
วิธีทำ จากสมการเส้นตรง y
= mx + c หา m , c
จากสมการปกติ
สร้างตาราง
แทนค่าในสมการปกติจะได้ …… = ……m + …..c………………….(1)
……... = ……m + ……c………………(2)
จากการแก้สมการจะได้ m = 0.636 , c
= 0.545
จะได้สมการของความสัมพันธ์คือ y = ……… x +……..
ถ้า x
= …..จะได้ y =
………(…) + …….. = ………….. พันบาท ซึ่งก็คือ…………….บาท
แสดงว่า ถ้ามีรายได้เดือนละ……………. บาท/เดือน
จะมีรายจ่ายประมาณ …………. บาท/เดือน
ค.
ถ้าครอบครัวหนึ่งในท้องที่นั้นมีรายจ่ายต่อเดือน 3,500 บาท จงทำนายรายได้ของครอบครัวนั้น
วิธีทำ ถ้าต้องการประมาณหรือทำนายค่าตัวแปรใดก็ต้องให้ตัวแปรนั้นเป็นตัวแปรตาม
และอีก
ตัวแปรหนึ่งเป็นตัวแปรอิสระ
โจทย์ต้องการทำนายค่าของ x แสดงว่า x เป็นตัวแปรตาม และ y เป็นตัวแปรอิสระ
สมการจะเปลี่ยนจาก y = mx
+ c เป็น x = my +
c และสมการปกติก็จะเปลี่ยนเป็น
แทนค่าในสมการปกติจะได้ 56
= 40m + 8c…………………(1)
364 = 256m + 40c……………….(2)
จากการแก้สมการจะได้ m = 1.5 , c = - 0.5
จะได้สมการของความสัมพันธ์คือ x = 1.5y - 0.5
แทนค่า y
= 3.5
จะได้ x = 1.5 (3.5)
- 0.5 = 4.75
ซึ่งมีค่าเท่ากับ 4,750
บาท
แสดงว่า ถ้าใช้จ่ายไปเดือนละ 3,500 บาท
จะมีรายได้เดือนละประมาณ 4,750 บาท
6.2.2
สมการความสัมพันธ์เชิงฟังก์ชันที่อยู่ในรูปพาราโบลา
สมการรูปทั่วไปของพาราโบลาคือ เมื่อ
a,b และ
c เป็นค่าคงตัว
x เป็นตัวแปรอิสระ และ y
เป็นตัวแปรตาม หาค่า a
, b และ c ได้จากสมการปกติ คือ
ตัวอย่างที่ 1 จากความสัมพันธ์ของข้อมูลต่อไปนี้
ก.
จงเขียนแผนภาพการกระจาย
ข. จงประมาณค่าของ y เมื่อ x = 10
เป็นสมการพาราโบลา หาค่าของ
a , b และ c ได้จากสมการปกติ
แทนค่าลงในสมการปกติ
|
30 = 140a + 28b+ 7c……………...(1)
121= 784a +
140b + 28c…………..(2)
647= 4676a +
784b + 140c………..(3)
4(1),
120 = 560a +112b +28c……………………(4)
(2)-(4), 1 = 224a +28b…………………………...(5)
20(1), 600
= 2800a + 560b +140c………………...(6)
(3)-(6), 47 = 1876a + 224b………………………..(7)
8(5), 8 = 1792a + 224b………………………..(8)
(7)-(8), 39 = 84a จะได้ a =
0.464
b = -3.676 , c =
9.71 จะได้สมการของความสัมพันธ์คือ
x เป็นตัวแปรอิสระ , y เป็นตัวแปรตาม
เพื่อให้สะดวกในการคำนวณ จะเปลี่ยนรูปของสมการใหม่โดยการใส่ log เข้าทั้งสองข้าง จะได้รูปของสมกา
ค.จงประมาณค่าของ x เมื่อ y = 10
ต้องการหาค่า x แสดงว่า x เป็นตัวแปรตาม และ y เป็นตัวแปรอิสระ
สมการรูปทั่วไปจะเปลี่ยนเป็น x = ay^2+by+c และสมการปกติจะเปลี่ยนเป็น
|
121= 810a + 148b + 30c…………….(2)
613=
4756a + 810b + 148c………….(3)
30(1), 840 = 4440a + 900b + 210c…………..(4)
7(2), 847 = 5670a + 1036b + 210c…………(5)
(5)-(4), 7 = 1230a + 136b…………………..(6)
74(2), 8954 = 59940 a+ 10952b + 2220c…….(7)
15(3), 9195 = 71340a + 12150b + 2220c……..(8)
(8) –(
7), 241= 11400 a + 1198b………………(9)
599(6)
, 4193 = 736770a + 81464b……………(10)
68(9), 16388 = 775200a + 81464b……………(11)
(11)-(10),12195
= 38430a
จะได้ a = 0.317
, b = -2.815 , c = 9.362
จะได้สมการของความสัมพันธ์คือ
ถ้า
y = 10 จะได้ x = (0.317)(100) + (-2.815)(10) +
9.362 = 12.912
.2.3 สมการความสัมพันธ์เชิงฟังก์ชันที่อยู่ในรูปเอกซ์โพเนนเชียล
ความสัมพันธ์เชิงฟังก์ชันที่อยู่ในรูปเอกซ์โปเนนเชียลจะมีสมการรูปทั่วไปคือ
x เป็นตัวแปรอิสระ , y เป็นตัวแปรตาม
เพื่อให้สะดวกในการคำนวณ จะเปลี่ยนรูปของสมการใหม่โดยการใส่ log เข้าทั้งสองข้าง จะได้รูปของสมการเป็น
ซึ่งจะได้ log y = log a + x log b
มีตัวไม่ทราบค่า 2 ตัวคือ log a กับ log b ซึ่งหาได้จากสมการปกติคือ
ตัวอย่างที่ 1 จากตารางแสดงการทดลองความเจริญเติบโตของต้นถั่วตามเวลาที่กำหนดได้ข้อมูล
ความสัมพันธ์ดังนี้
|
ก.
จงเขียนแผนภาพการกระจาย
ข.
ในสัปดาห์ที่ 10 ต้นถั่วจะสูงประมาณกี่เมตร
วิธีทำ เนื่องจากความสัมพันธ์เป็นเอกซ์โพเนนเชียลจะได้สมการรูปทั่วไปคือ
log y =
log a + x log b หาค่า log
a และ log bจากสมการปกติคือ
แทนค่าในสมการปกติจะได้ 7.2878 = 36 log b + 8 log a…………………..(1)
44.5884 =
204 log b + 36 log a………………..(2)
จากการแก้สมการจะได้ log a = -0.3583 , log b = 0.2818
จะได้สมการของความสัมพันธ์คือ log
y = - 0.3583 + 0.2818 x
ถ้า x = 10
จะได้
log y
= - 0.3583 + 0.2818 (10)
= -0.3583 + 2.818 = 2.4597
Anti log y จะได้ y = 288 เพราะฉะนั้นในสัปดาห์ที่ 10
ต้นถั่วจะสูงประมาณ 288 ซม.
หรือเท่ากับ 2.88 เมตร
6.3 ข้อมูลที่อยู่ในรูปอนุกรมเวลา
ได้แก่ข้อมูลซึ่งแต่ละค่าของข้อมูลเกิดขึ้นตามช่วงเวลา
โดยทั่วไปแล้วมักจะเป็นช่วงเวลาที่เท่ากัน
ดังนั้นข้อมูลที่เกิดขึ้นจะต้องมีความสัมพันธ์เชิงฟังก์ชันกับเวลา
ถ้าให้ข้อมูลที่สนใจศึกษาคือ y
และระยะเวลาคือ x จะได้ความสัมพันธ์คือ
เมื่อ x คือตัวแปรอิสระ
และ y คือตัวแปรตาม
การแทนค่า x ในเรื่องของเวลา
-
ถ้าจำนวนเวลาเป็นจำนวนคี่ ให้แทนค่าเวลาด้วยค่า x ดังนี้
-
ถ้าจำนวนเวลาเป็นจำนวนคู่ ให้แทนค่าเวลาด้วยค่า x ดังนี้
ตัวอย่างที่ 1 ข้อมูลต่อไปนี้แสดงจำนวนภาษีที่บริษัทแห่งหนึ่งต้องชำระให้แก่กรมสรรพากร
ตั้งแต่ปี พ.ศ.
2529 – 2534
ก.
จงเขียนแผนภาพการกระจาย
วิธีทำ
ข. จงทำนายภาษีที่บริษัทแห่งนี้ต้องชำระให้แก่กรมสรรพากรในปี
พ.ศ. 2535 และพ.ศ.2540
แทนค่าในสมการปกติ ….. = ….. ……………(1) จะได้ ……. = ………
……. = …… …………..(2) จะได้ …… = ………
จะได้สมการของความสัมพันธ์คือ y = ……….x + ………….
ปี พ.ศ. 2535 แทน x ด้วย ………
จะได้ y = ………. …+
…………..=…. …………………
ปี พ.ศ. 2540 แทน x ด้วย ……… จะได้ y = …………..+ …….. ……=……………………
ตัวอย่างที่ 2 ข้อมูลต่อไปนี้แสดงเนื้อหมูโดยเฉลี่ย(กก.) ที่แต่ละคนในท้องที่แห่งหนึ่งบริโภคต่อปี
ในระหว่าง
พ.ศ. 2526 ถึง พ.ศ. 2534
ก.
จงเขียนแผนภาพการกระจาย
|
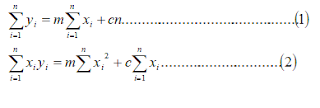
ไม่มีความคิดเห็น:
แสดงความคิดเห็น